海边别墅

# 算法基础

# java中的数据结构

哈希表： https://www.cnblogs.com/chen-lhx/p/8432422.html

  • HashMap（无序，允许Key、value为null）
  • TreeMap（有序，默认Key升序）
  • LinkedHashMap（有序，按插入顺序记录）
  • LinkedList（有序集合）

# TreeMap的使用

# 复杂度

# 时间复杂度

# 参阅

时间复杂度中的log（n）底数到底是多少？ (opens new window) O(log n) 怎么算出来的 (opens new window) 时间复杂度 O(log n) 意味着什么？ (opens new window)

# 空间复杂度

# 双指针

遍历右指针，左指针同时向右收缩：713. 乘积小于K的子数组 (opens new window)

# 图

# 图（graph）中的几个基本概念

  • 顶点（vertex）：图中的元素节点
  • 边（edge）：两个顶点间存在的连接关系
  • 度（degree）：与顶点相连接边的条数
    • 入度：有多少条边指向此顶点
    • 出度：有多少条边是以此顶点为起点指向其他顶点
  • 带权图
  • 稀疏图、稠密图

# 如何存储图？

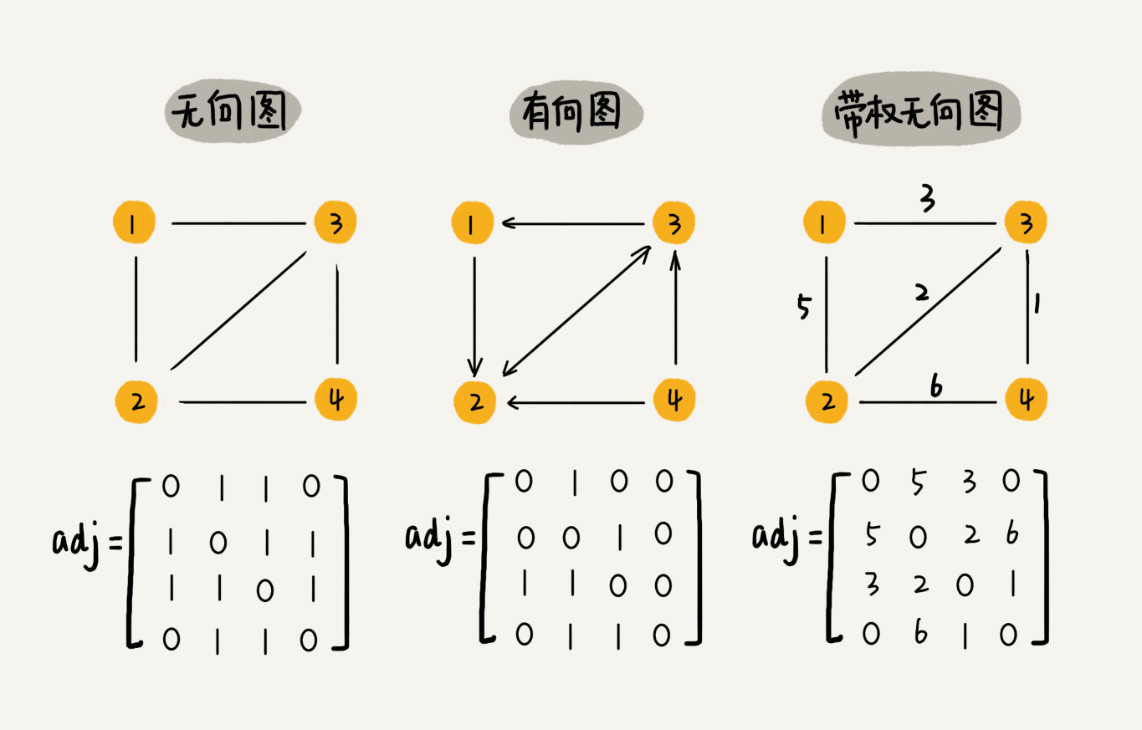
邻接矩阵

使用二维数组存储图，adj[A][B] = 1二维的两个下标表示从节点A到节点B存在一个有向边，若是无向图，则需要反过来同样表示adj[B][A] = 1。

邻接矩阵的优点是简单，缺点是浪费空间，若是稀疏图，则非常浪费空间。

image-20210802224243102

邻接表、逆邻接表

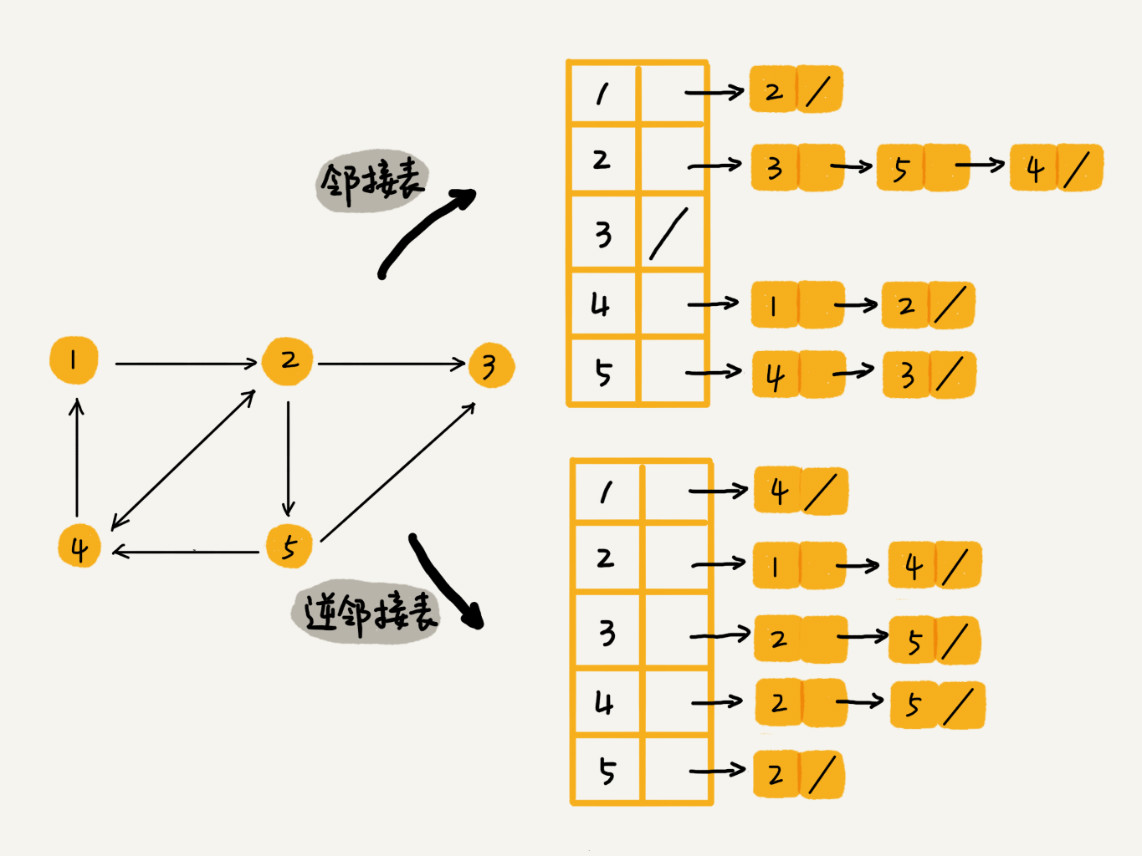
使用Map<Integer, List<Integer>>的结构存储，顶点作为hash表的key，与顶点相连的所有节点都存储到链表中。

邻接表可以很方便的查找一个顶点为起点，指向了多少个其他顶点，但是无法方便知道有哪些顶点指向某一个顶点，因此就有了逆邻接表。

逆邻接表中，同样是顶点作为hash表的key，但值是存储了所有指向顶点key的节点。

邻接表比邻接矩阵节约空间，但查找效率不及邻接矩阵，不过可以加红黑树优化（或者平衡二叉树、跳表、散列表等）。

image-20210802225105209

大数据量常见如何存储图？

利用数据分片，将顶点分片存储。

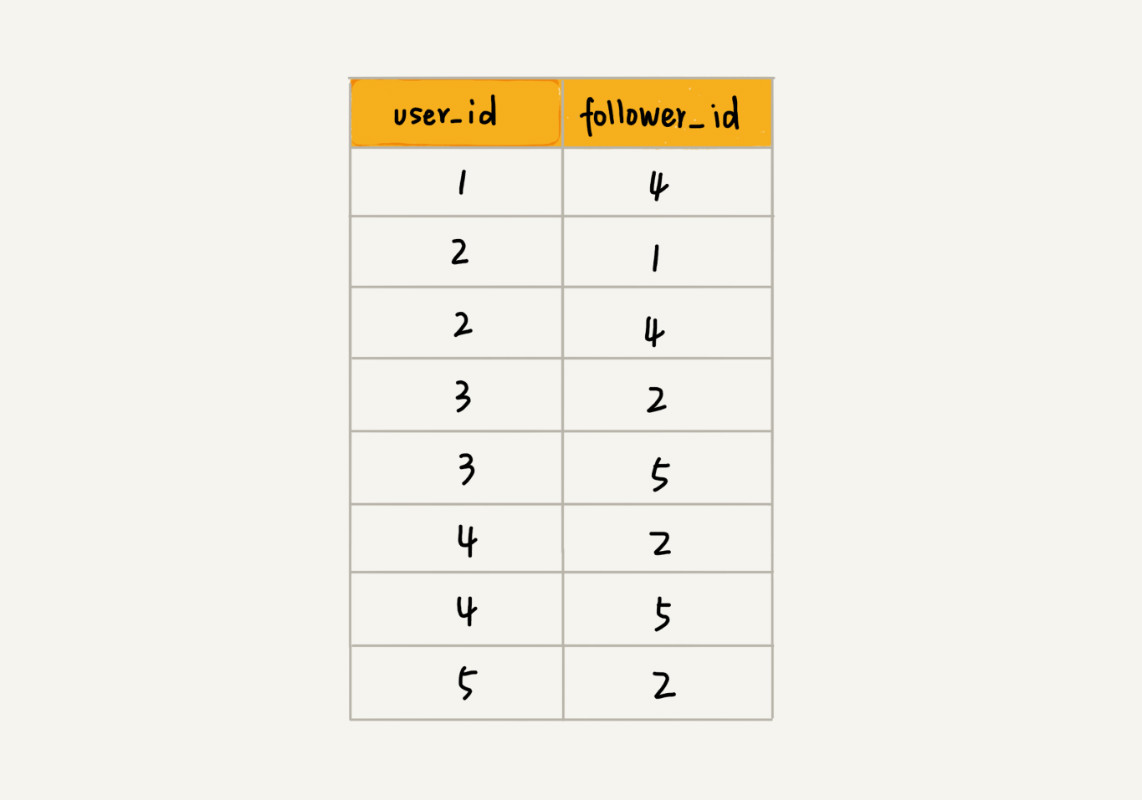
关系型数据库如何存储图？

image-20210802231745157

# 如何遍历图？

通常使用

  • BFS
  • DFS

# 如何判断一个有向图是否存在环？

  • 快慢指针（单向边找环）
  • 递归、dfs
  • 拓扑排序

# 栈

# 单调栈、单调队列

单调栈：指从栈顶到栈底是严格递增还是严格递减的栈。

  • 单调递增

    • [5,4,3,2,1] 左边栈底，右边栈顶
    • 当前元素 >= 栈顶元素，弹出栈顶元素，直到小于时，将当前元素放置栈顶。
    • 当前元素 < 栈顶元素，放置栈顶。
    • 如果向右遍历数组，能在栈中找到左边第一个大于当前元素的值。

  • 单调递减

    • [1,2,3,4,5] 左边栈底，右边栈顶
    • 当前元素 <= 栈顶元素，弹出栈顶元素，直到大于时，将当前元素放置栈顶。
    • 当前元素 > 栈顶元素，放置栈顶。
    • 如果向右遍历数组，能在栈中找到左边第一个小于当前元素的值。

# 回溯

回溯其实就是一种枚举，回溯一般可以构造成一个递归树。

求解组合问题时，如果要求解集不能重复，需要排序，相同的跳过相同的元素。

【46. 全排列】是典型的回溯算法题，其实是构建一个递归树

# 枚举

  • 枚举三个数时，使用三层循环嵌套，每一层的指针起始位置等于上一层+1

    for i := 0; i < n; i++ {
    for j := i+1; j < n; j++ {
        for k := j+1; k < n; k++ {
            
        }
    }
}

# 优先队列

# 例题

# 两个双端队列动态获取区间内最值

# 并查集

  • 可以用来判断图中是否有环
  • 统计分组数

# 并查集相关题目

  • 684. 冗余连接
  • 547. 省份数量

# 并查集模板

count记录孤立集合有多少，parent数组表示领头元素集合。

class UnionFind {
    private int count = 0;
    private int[] parent;
    
    public UnionFind(int n) {
        count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    public int find(int p) {
        while (p != parent[p]) {
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;
    }
    
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    
    public void union(int p, int q) {
        int rp = find(p);
        int rq = find(q);
        if (rp == rq) return;
        parent[rp] = rq;
        count--;
    }
}

# 前缀和

# 前缀和题目

  • 274. H 指数

# 二分法、二分查找

移步：搜索算法 (opens new window)

# 拓扑排序

toposort

算法实现有：Kahn算法、DFS

# kahn算法（贪心）

pre[0] = {0, numcourses-1} pre[1] = {0, numcourses-1}

map<n, degree> 统计入度

找出0度的，从0度的数开始，将其指向的所有数拿出来，每当一个顶点为0时，加入计数，并重复以上步骤，拿出其所有指向的数出来。

public void toposortByKahn() {
  int[] inDegree = new int[v]; // 统计每个顶点的入度
  for (int i = 0; i < v; ++i) {
    for (int j = 0; j < adj[i].size(); ++j) {
      int w = adj[i].get(j); // i->w
      inDegree[w]++;
    }
  }
  LinkedList<Integer> queue = new LinkedList<>();
  for (int i = 0; i < v; ++i) {
    if (inDegree[i] == 0) queue.add(i);
  }
  while (!queue.isEmpty()) {
    int i = queue.remove();
    System.out.print("->" + i);
    for (int j = 0; j < adj[i].size(); ++j) {
      int k = adj[i].get(j);
      inDegree[k]--;
      if (inDegree[k] == 0) queue.add(k);
    }
  }

# 拓扑DFS

# 拓扑排序题目

802. 找到最终的安全状态 (opens new window) 207. 课程表 210. 课程表 II 457. 环形数组是否存在循环

# 动态规划

  • 序列DP
  • 区间DP
  • 数位DP

# 常用标记方式-数组

# 用数组做映射和哈希表

# 如果数组两两比较，循环时从下标1开始，可以避免最后多余判断

# 解题时，懵逼时怎么办

  • 想想有没有暴力解（朴素解）
  • 简化问题，罗列基本情况，找最近的、重复的子问题，或者说寻找可以优化的过程。
  • 分析需要优化的过程，先列出需要哪些特性，再思考哪些数据结构可以提供这些特性（仍然需要熟悉数据结构的特性）。
  • 需要了解Java针对各种数据结构所提供的支持。
  • 平时要多练习将题意转成另一种方便理解的变种，或者其他原题。

# 进制、数制

十进制使用最为广泛的原因与人类有10个手指头是密不可分的。

在我国古代使用过十六进制，成语半斤八两指的是八两是半斤，一斤就是十六两，也就是以十六为基数。

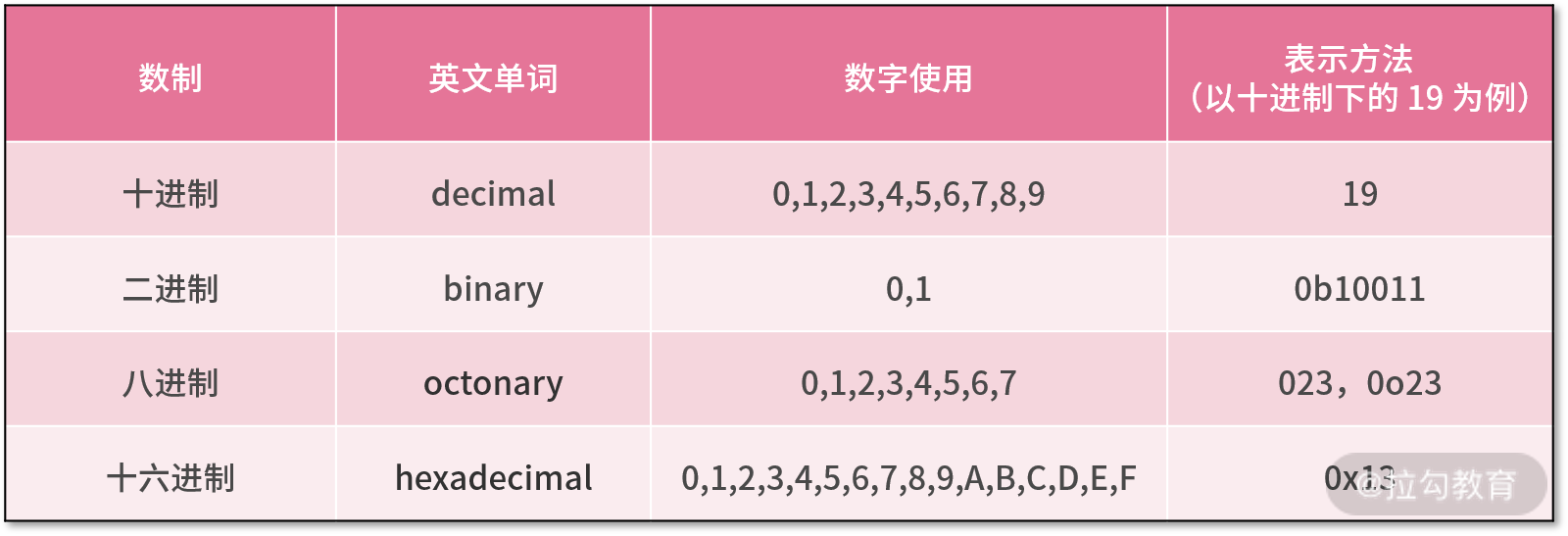
不同进制的前缀表示：

  • 没有前缀表示的一般为十进制
  • 二进制：0b
  • 八进制：0o或0
  • 十六进制：0x

b、o、x分别是各自数制的英文单词：binary、octonary、hexadecimal

十进制英文：decimal

image-20210802233106135

# 进制转换的方法

1.换基法

2.除余法

3.按位拆分法、按位合并法

4.数制转换图

# 位运算

# 位运算方式=按位运算

按位运算符针对布尔值与逻辑运算符效果一样, 但是不会出现短路的情况.

按位运算满足交换律和结合律

# 异或运算

相同的为0, 不同的为1, 因此被称为不进位的二进制加法.

异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1） 且满足交换律 （即不进位加法） 任何数与1异或，奇数-1，偶数+1。 任何数与自己异或皆为自己。 自己与自己异或

异或的效果:

  1. x^0

无论x为什么, 都值都保持不变.

  1. x^1

结果是将x值进行翻转

  1. x^x

结果为0

异或运算的用法:

  1. 判断两个值是否相等

a^b=0则a与b相等, 因为必须每一位都相等, 最后结果才可能为0.

  1. 指定某位进行翻转

a. 将需要翻转的位设为1, 目标值与设定值进行^

b. 0或1的数取反使用异或^1

  1. 交换两个值(不需要临时变量)
a=a^b
b=b^a
a=a^b
  1. 用于加密解密

用一个字符x对其原文的每一个小单位进行^, 则是加密, 再重复同样操作则是解密.

假设: result=a^x
则result^x=a^x^x, result^x=a;

# 与运算

只要有一个为0就为0

与运算作用:

  1. 将某一位清零(置0)

与运算的用法：

  1. 去掉最低位的1

    n = n & (n-1);
// 或者写作
n &= (n-1);

# 或运算

只要有一个是1, 则为1

或运算的效果:

  1. x|0

无论x为什么, 都值都保持不变, 这一点与异或^相同.

或运算用法:

  1. 常用于关闭位, 将指定位置1

# 非运算

进行取反, ~0=1, ~1=0

# 与等号一起的组合运算符

与关系运算一样, 可以配合=一起使用, 用于合并运算及赋值

1. &=

为什么&=是获得余数??

2. |=

为什么|=是没满右侧的数字则是右侧数字减一(右侧是1023则是这样).

# 移位运算

# 左移位

左移位规则: 丢弃最高位, 最低位补0. 左移位的意义: 在没有溢出的前提下, 左移n位, 等于乘以2的n次方.

value << num

value为被移位值 num是移动位数

# 位运算在日常开发中的使用

  1. &用来减去一定值. 因为&可以将某一位置0, 所以可以达到减法的效果.

  2. |和<<用来赋值 x|0结果不变, 所有可以用来赋值操作, 然后移位, 补零之后继续赋值.

  3. 利用一个int字段存储二进制数据, 一个字段就可以表示n个属性 设计一个指定长度的二进制数据, 并将每一段设计为表达不同的内容, 利用<<和|来组合内容. 利用&来拆分/取出数据. int type = (1<<31) | (1<<16) |5

  4. 用二进制数代替数组或者map。 假设需要标记小写英文字母在一个数组中是否出现过，可以使用26位的二进制数标记：mask |= 1 << int_char

  5. 两个数字进行或运算，相当于两个数每一个有1的位都会使用结果的对应位为1，可以理解成合并两个数。

  6. 可以通过&运算将一个数限制在(2^n)-1大小的范围内，该结果通过可以用作数组的下标（这就要求数据的大小是2^n），也就是针对数组取模。

    参考Java中的ThreadLocal代码int i = key.threadLocalHashCode & (len-1);，i就是对key的hashcode取模后找到在数组中的位置。

# 其他资料

二进制表示一个棋盘 (opens new window)

# TopK问题

解决该问题有很多方法：

  1. 先排序，后遍历 O(nlogn)
  2. 优先队列、小顶堆 O(nlogk)
  3. 快速选择算法 平均O(n) 最坏O(n^2)
  4. BFPRT 最坏 O(n)

# 快速选择算法 求TopK

平均时间复杂度为O(n)

假设数组是已排序的，并且每次取pivot都是用最小的或者最大的，搜索范围只能缩小1，因此最坏时间复杂度为O(n^2)

快速选择只能找第k个，不能在包含重复数据的数组中找第k大的元素，但可以先去重。

public class QuickSelect {
    public int quickSelect(int[] nums, int k) {
        return quickSelect(nums, k, 0, nums.length-1);
    }

    public int quickSelect(int[] nums, int k, int lo, int hi) {
        // [hi,lo]中随机取一个
        int p = (int)Math.floor(Math.random() * (hi-lo+1)) + lo;
        // 交换pivot到最高位
        swap(nums, p, hi);
        // 定义双指针i、j
        // 当j元素小于等于hi元素，交换i与j元素，i与j下标同时右移一位
        // 当大于时，仅j下标右移一位
        // 当遍历完一次后，所有小于等于hi元素的都在i下标的左边，i下标右边为大于hi元素的数
        int i = lo, j = lo;
        while (j < hi) {
            if (nums[j] <= nums[hi]) {
                swap(nums, i, j);
                i++;
            }
            j++;
        }
        // 交换元素，以i为中心，左边都是小于等于i的，右边皆为大于i的
        // 判断i是否为第k大的元素，如果不是，搜索范围缩小到左边或者右边继续递归
        swap(nums, i, hi);

        if (i+k-1 == hi) return nums[i];

        if (i+k-1 > hi) return quickSelect(nums, k-(hi-i+1), lo, i-1);

        return quickSelect(nums, k, i+1, hi);
    }

    public void swap(int[] nums, int a, int b) {
        int tmp = nums[a];
        nums[a] = nums[b];
        nums[b] = tmp;
    }

    public static void main(String[] args) {
        QuickSelect qs = new QuickSelect();
        int res = qs.quickSelect(new int[]{3,2,1,5,6,4}, 3);
        System.out.println(res);
    }
}

# 竞赛

# 算法课程

慕课网-yubobobo

# 数算

# 两位数乘法

十位数相同，个位数相加等于0时：

xy1*xy2 = x*(x+1) 拼接 y1*y2
例如：
45*45 = 4*5 拼接 5*5 = 2025
43*47 = 4*5 拼接 3*7 = 2021
修改于: 8/11/2022, 3:17:56 PM

←